Characterizing quantum bilocal networks with generalized NPA hierarchies
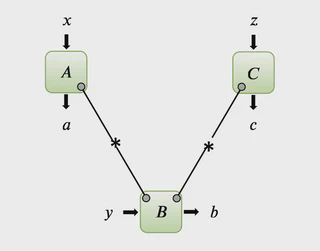 Image credit: myself :D
Image credit: myself :DAbstract
Characterising the correlations that arise from locally measuring a single part of a joint quantum system is one of the main problems of quantum information theory. The seminal work [M. Navascu´es et al, NJP 10,7,073013 (2008)], known as the NPA hierarchy, reformulated this question as a polynomial optimisation problem over noncommutative variables and proposed a convergent hierarchy of necessary conditions, each testable using semidefinite programming. More recently, the problem of characterising the quantum network correlations, which arise when locally measuring several independent quantum systems distributed in a network, has received considerable interest. Several generalisations of the NPA hierarchy, such as the Scalar Extension [Pozas-Kerstjens et al, Phys. Rev. Lett. 123, 140503 (2019)], were introduced while their converging sets remain unknown. In this work, we introduce a new hierarchy, prove its equivalence to the Scalar Extension, and characterise its convergence in the case of the simplest network, the bilocal scenario, and explore its relations with the known generalisations.
This talk has been presented at multiple venues. The date above is set to the most recent instance for correct ordering in the Talks list. Materials (slides/poster) are shared with minor venue-specific tweaks.
Talks
| Date | Event | Host / Location | Type |
|---|---|---|---|
| 2024-09 | CausalWorlds1 | Perimeter Institute, Waterloo (CA) | Contributed |
| 2023-11 | Defi EQIP2 | Inria Lyon, Lyon (FR) | Contributed |
| 2023-10 | Saclay Quantum Seminar | Inria Saclay, Palaiseau (FR) | Invited |
Poster sessions
| Date | Event | Host / Location |
|---|---|---|
| 2024-11 | YQIS243 | Inria Paris, Paris (FR) |
| 2024-11 | GDR TeQ 20244 | Sorbonne University, Paris (FR) |
Also presented at various internal group meetings during research visits.

Image credit: WAQ (We are quantum) at Paris, France

Image credit: YQIS24 at Paris, France